Die Datenmatrix für die Analyse

Für unser Beispiel benutze ich die cars Datenmatrix, die mit der Statistik-Software R standardmäßig mitgeliefert wird.

Diese Datenmatrix enthält zwei Spalten und 50 Zeilen, und präsentiert den Bremsweg eines Autos (Spalte: dist) in Abhängigkeit von seiner Geschwindigkeit (Spalte: speed).

Die Daten wurden in den 1920-er Jahren gesammelt und sind dementsprechend nicht wirklich aussagekräftig für die heutigen Umstände, allerdings haben diese Daten spezifische Eigenschaften, die durchaus auch heutzutage von Interesse sind.

Unten ist das Streudiagramm dieser beiden Variablen zu sehen.

Ich habe hier als Datenmarker ein Auto-Symbol (Webdings) benutzt, was sicherlich unterhaltsam wirkt, ohne dabei die Datendarstellung zu verzehren oder die Wahrnehmung der Information in irgendeiner Weise zu hindern. 

Als Erstes fällt die inhomogene Streuung der Werte entlang der Y-Achse in Bezug auf die verschiedenen Abschnitte der X-Achse auf.

In der Grafik unten sind beide Bereiche der inhomogenen Streuung mit den farblichen Rechtecken markiert:

Dieser Umstand wird als Heteroskedastizität bezeichnet und hat zur Folge, dass die Annahmen über die Modellierung mittels der einfachen OLS-Schätzung stets verletzt werden und das OLS-Modell inkonsistente und nicht erwartungstreue Schätzer liefern wird.

Dementsprechend kann man auf diese Weise das lineare Modell nicht bilden.

Um dieses Hindernis zu umgehen, empfiehlt sich, die Variablen-Transformation vorzunehmen, sodass die OLS-Schätzung für die Modellbildung dann doch benutzt werden kann.

Ich habe für diesen Zweck die Quadratwurzeln aus beiden Variablen gezogen und anschließend diese im Streudiagramm dargestellt. Man sieht, dass die Varianz entlang der Y-Achse in Bezug auf die unterschiedlichen Abschnitte der X-Achse jetzt viel homogener geworden ist:

Regressionsanalyse mittels OLS in R

Jetzt ist es an der Zeit, das Modell mithilfe der Methode der kleinsten Quadrate (OLS)  anhand dieser modifizierten Daten zu bilden und anschließend zu evaluieren.

Hierfür wäre ein Testset notwendig gewesen. Deshalb werde ich fünf Datensätze aus der Datenmatrix entnehmen und nicht für die eigentliche Modellierung verwenden, sondern beiseitelegen und später für das Evaluieren des entstandenen Modells benutzen.

In der Grafik unten wurden die fünf "Autos" rot markiert, die nicht zur Modellierung verwendet werden, sondern aus den Daten entnommen und anschließend als Testset benutzt:

Man sieht, dass das Modell durchaus adäquat ist, besonders gut ist es allerdings dann doch nicht wirklich.

Die relativ hohe Streuung der Werte um die Modell-Kurve kann mithilfe einer linearen Beziehung partout nicht umfassend abgedeckt werden, selbst wenn die Heteroskedastizität im Vorfeld eliminiert wird.

Man kriegt dadurch zwar konsistente Schätzer, anhand dessen man erwartungstreue Konfidenzintervalle bilden kann, die Variabilität der abhängigen Variable bleibt aber nicht besonders gut erfasst. Das vorliegende lineare Modell deckt lediglich ca. 71 % der Varianz vom Bremsweg eines Autos in Abhängigkeit von seiner Geschwindigkeit ab.

Die restlichen ca. 29 % der Varianz können nicht anhand einer einzigen unabhängigen Variable erklärt werden. Hier fehlt offensichtlich noch eine latente Variable oder mehrere, die in unseren Daten einfach nicht vorhanden sind.

Dies kann vermutlich das Gewicht eines Autos sein und / oder andere Faktoren, etwa der Reifentyp, etc.

Es ist daher die Aufgabe eines Analytikers stets die Plausibilität des Modells und der Daten zu überprüfen und ggf. die zusätzlichen Merkmale in das jeweilige Modell mit aufzunehmen.

• speed = Geschwindigkeit
• dist = Bremsweg
• Predicted Value = Vorhersage des Bremsweges in Abhängigkeit von der Geschwindigkeit

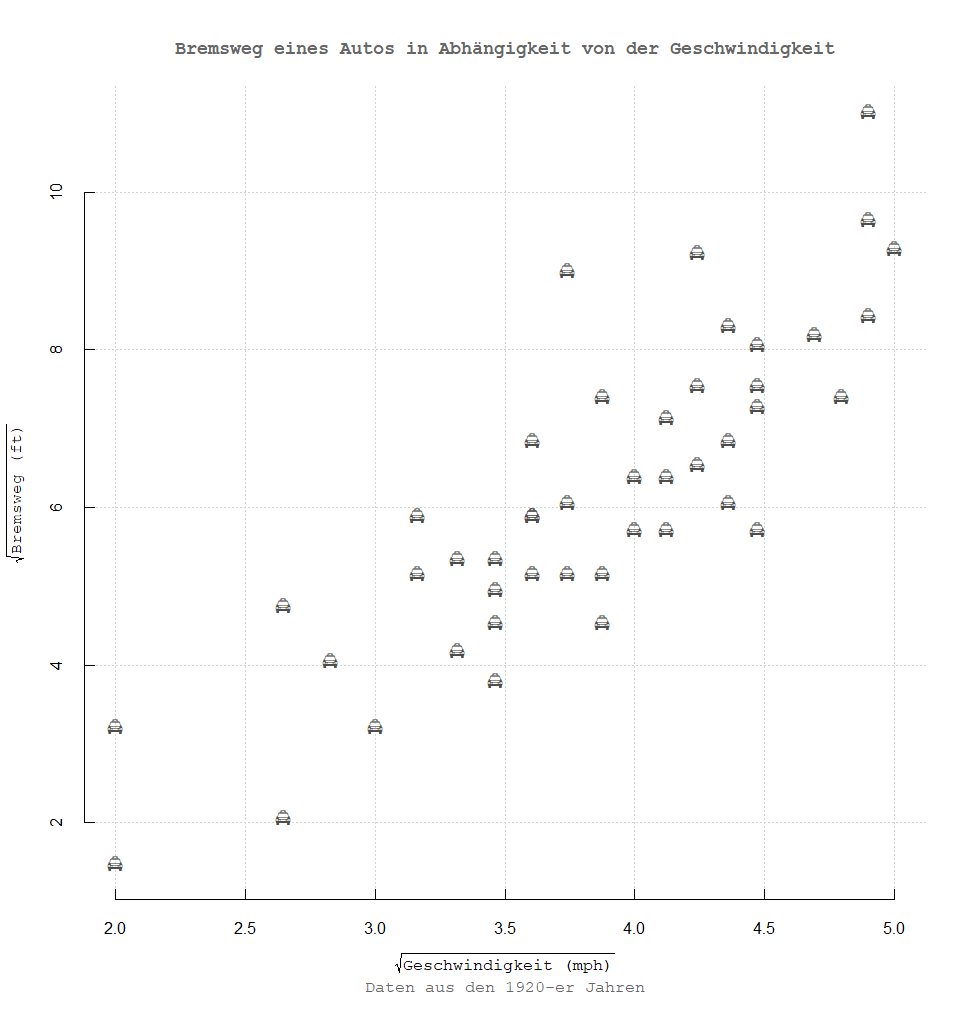
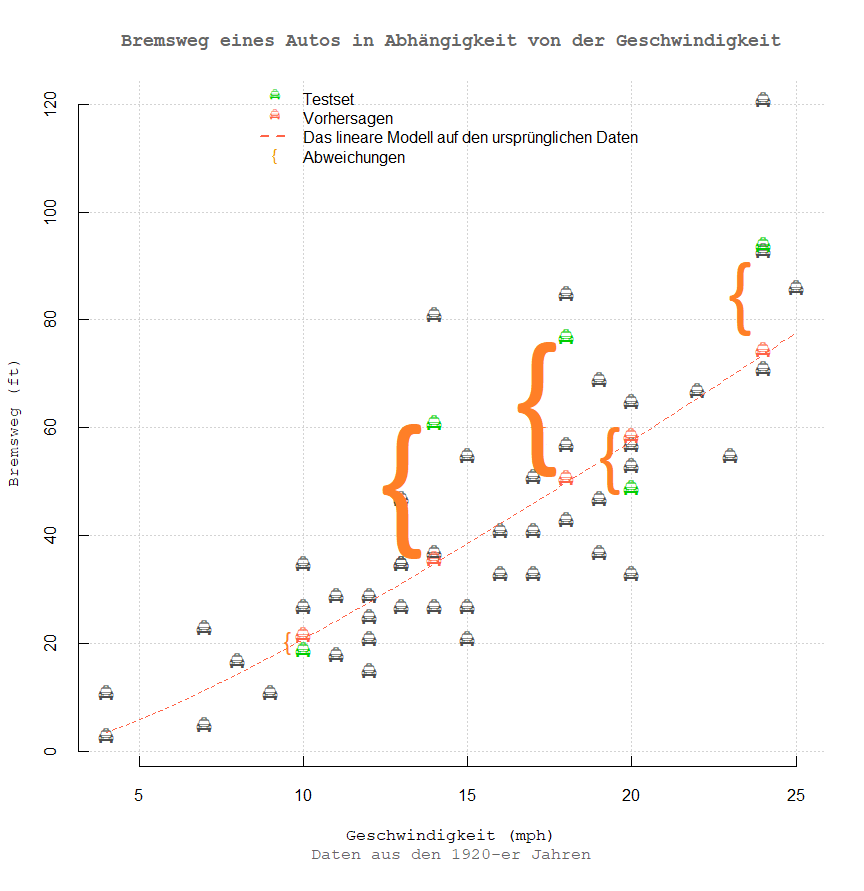
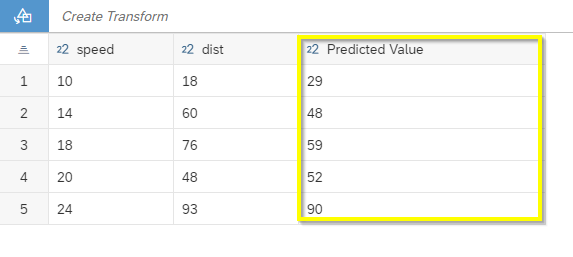
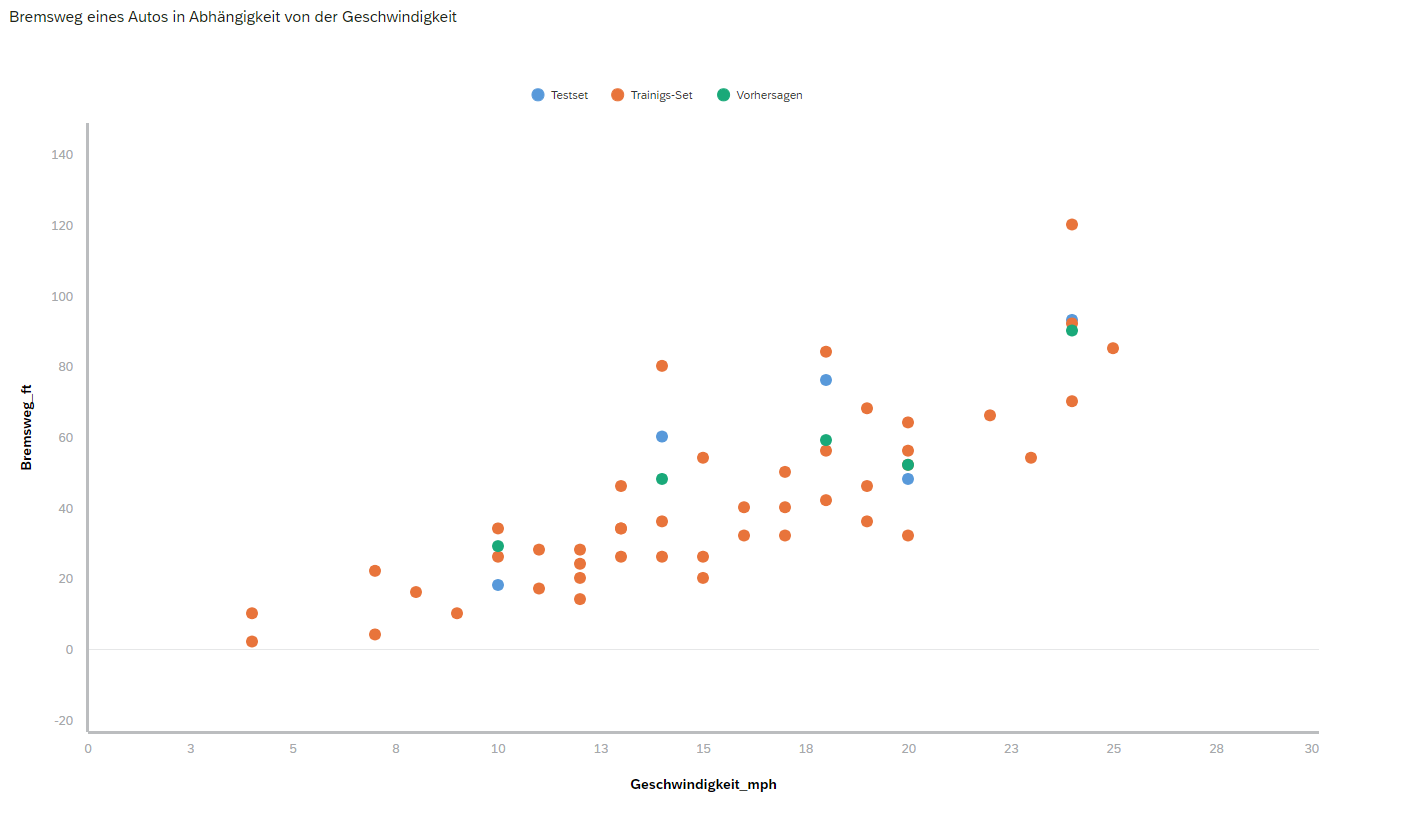
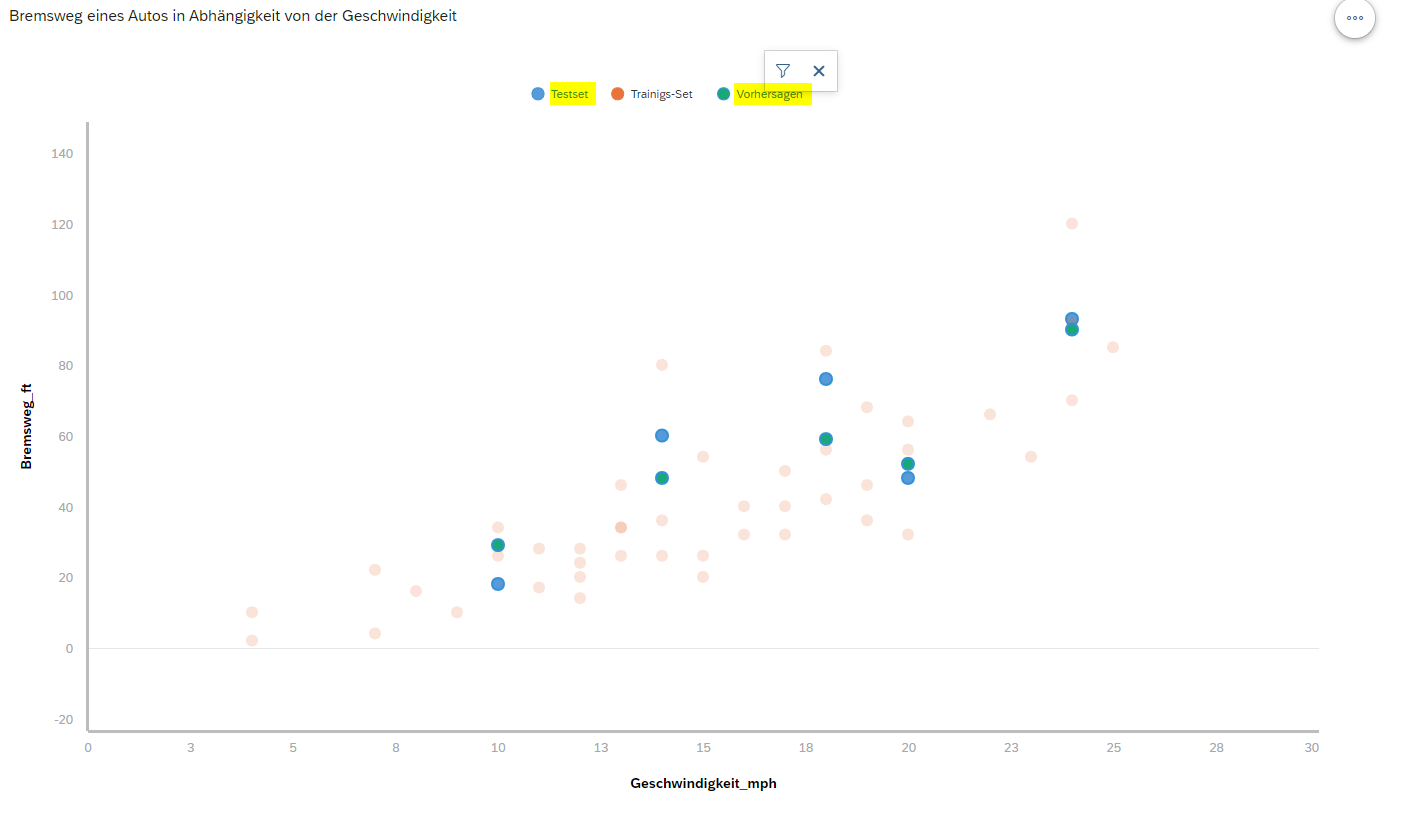
Die Error Metriken für diese Vorhersagen sehen folgendermaßen aus:

RMSE:  10.76104

MAE:     9.4

MAPE:   0.2300773

Man sieht, dass diese Werte eine Verbesserung an sich darstellen im Vergleich mit den Error Metriken, die wir oben in R mithilfe einfacher linearer Regression erzielt haben: MAPE von 0.27 in R vs. 0.23 in der SAC.

Das ist auch nicht verwunderlich, da der nicht-parametrische Gradient Boosting Regressionsbaum, der in SAC verwendet wird, nicht an einen linearen Zusammenhang in den Daten gebunden ist und daher viel flexibler und dementsprechend effizienter agieren kann.

Besonders ist es auffällig, wenn die Variabilität der Residuen um ihren Mittelwert (Null-Wert) hoch ist, - was bei diesem Datensatz tatsächlich der Fall ist.

In solchen Fällen wird ein nicht-parametrischer Ansatz (was in SAC benutzt wird) den parametrischen (linearen) Ansatz (fast) immer schlagen.

Selbst wenn die Heteroskedastizität für das lineare Modell eliminiert wurde, variieren die Residuen dennoch sehr stark um ihren Mittelwert (Varianz der Residuen ist zwar stationär geworden, dennoch ist die Streuung zu hoch) - was von einer Unvollständigkeit des gewählten Modells spricht - und dementsprechend kann das einfache lineare Modell diese hohe Streuung auch nicht kohärent erfassen.

Der nicht-parametrische Ansatz eines Regressionsbaums (SAC Modell) wäre hier tatsächlich die richtige Wahl gewesen.

Dennoch beträgt die Minderung beim durchschnittlichen prozentualen Fehler (MAPE) lediglich ca. 3,5 Prozentpunkte (vgl. oben mit MAPE für OLS in R), was nicht sonderlich nach einer signifikanten Verbesserung des Modells klänge. 

Dieser Umstand bestätigt lediglich die These, dass man zusätzliche Merkmale in das Modell aufnehmen soll, um die Streuung der abhängigen Variable besser erfassen zu können, und erst danach ein statistisches Modell bilden.   

Fazit

Die Regression ist ein sehr mächtiges Werkzeug und kann mittels sehr unterschiedlicher Techniken bewerkstelligt werden.

Die Statistik-Software R beherrscht alle existierenden Verfahren, von einem einfachen linearen Modell aus diesem Blogbeitrag, bis hin zu sehr komplexen Verfahren, die mithilfe vom stochastischen Gradientenabstieg die neuronalen Netze mit mehreren versteckten Schichten trainieren und die Regressions-Aufgaben lösen können.

Man ist in R sehr flexibel, wenn es um die Auswahl einer bestimmten Technik geht, denn alles kann auch in R nachgebaut werden.

In der SAC hat man im Gegensatz dazu, ausschließlich die Methode(n) verfügbar, die dort implementiert wurde(n). Man ist quasi an diese einzige vorkonfektionierte Lösung gebunden.

Dennoch sind in vielen Situationen die SAC Lösungen ausreichend gut genug, um die Predictive Analytics Szenarien zu verwirklichen.

In diesem Sinne: viel Spaß beim Modellieren!