Paired Samples T-Test
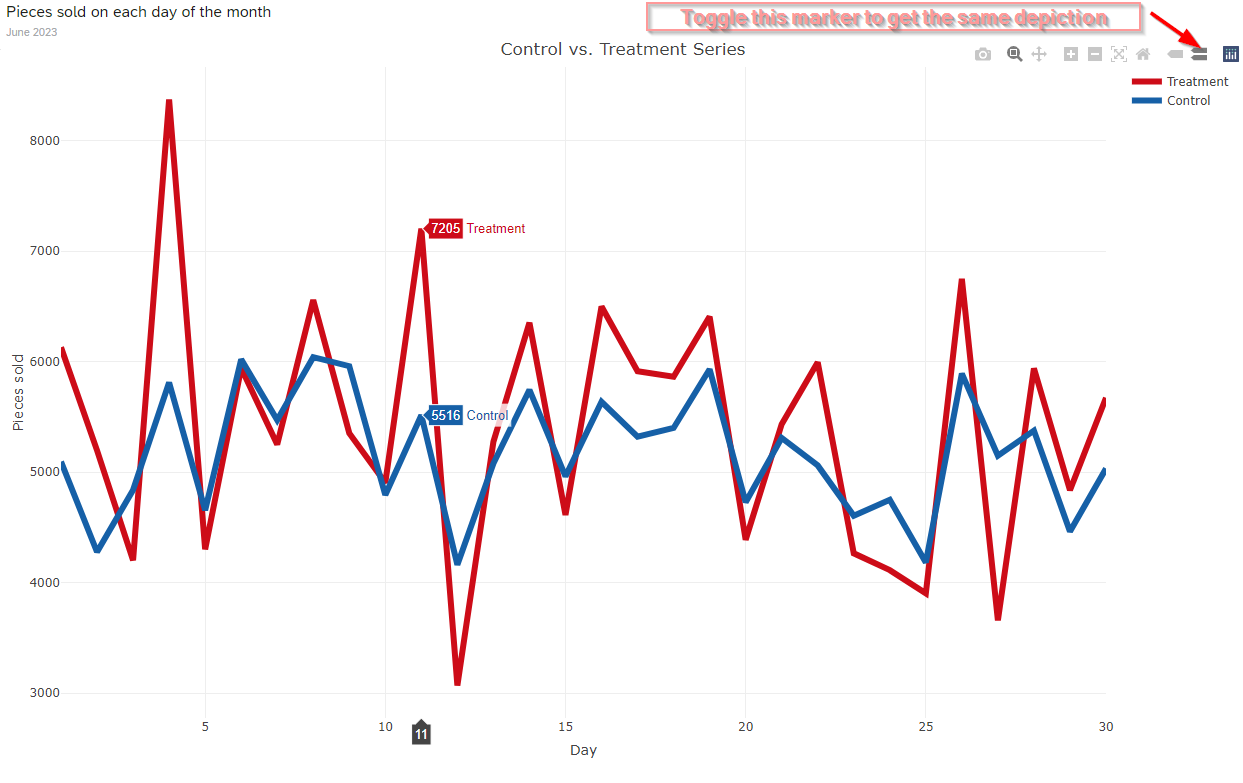
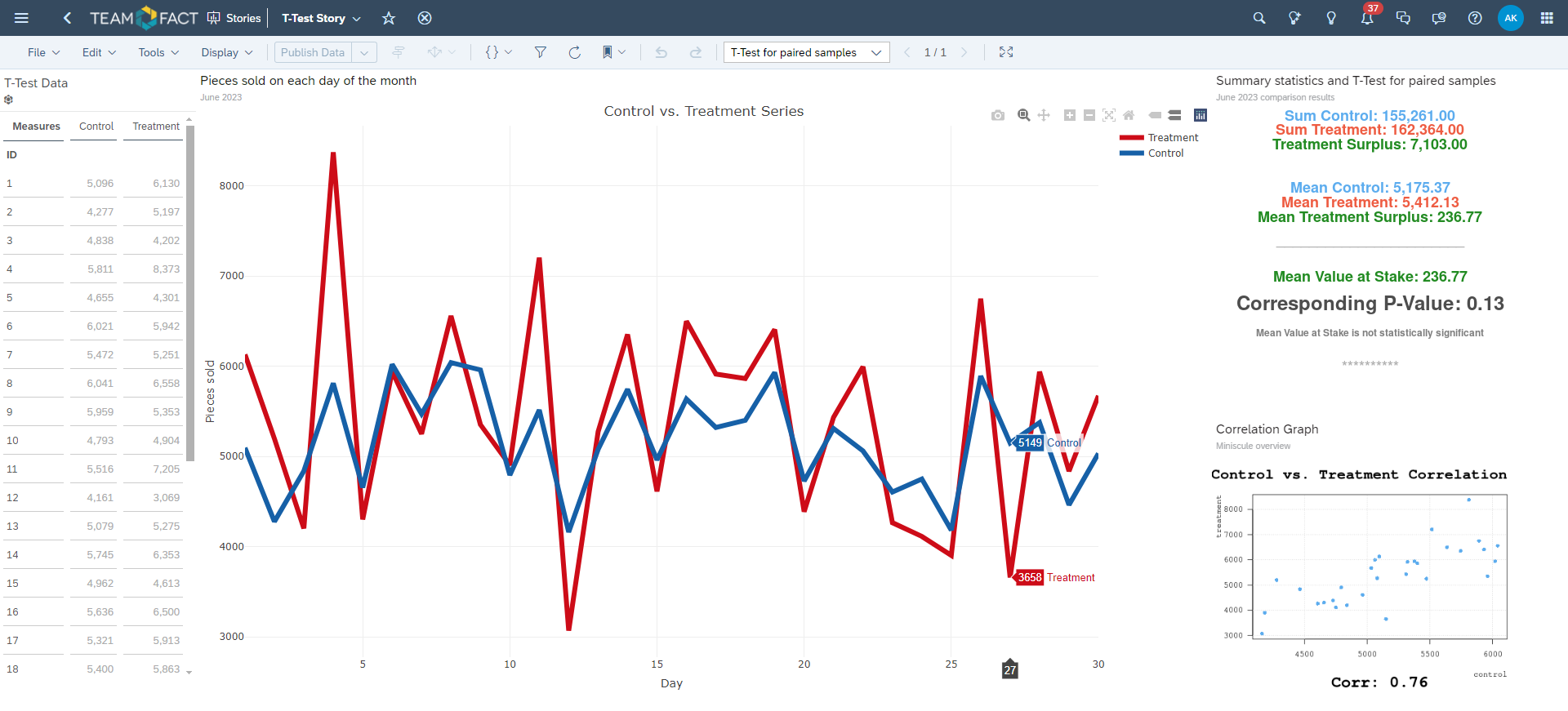
So, let's actually conduct this paired samples T-Test and depict its results in a graphical way inside an R Widget.
The Code to accomplish this is presented below:
----
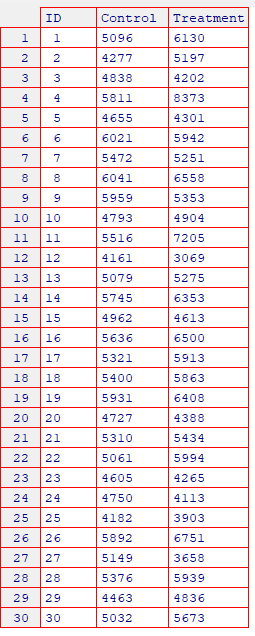
dta <- ttest_data
dta$ID <- as.character(dta$ID)
dta$ID <- as.numeric(dta$ID)
control <- dta$Control
treatment <- dta$Treatment
par(mar = rep(0, 4))
plot(NA, NA, xlim = c(0, 1), ylim = c(0, 1), ann = FALSE, axes = FALSE)
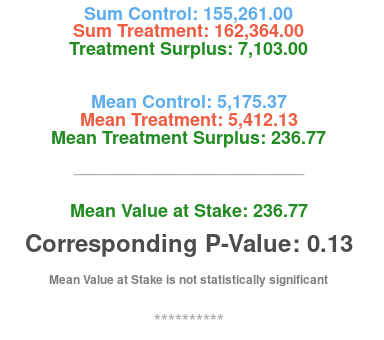
text(0.5, 1.0, paste0("Sum Control: ", format(sum(control), nsmall = 2, big.mark = ",")), xpd = TRUE, font = 2, cex = 1.5, col = "steelblue2")
text(0.5, 0.95, paste0("Sum Treatment: ", format(sum(treatment), nsmall = 2, big.mark = ",")), xpd = TRUE, font = 2, cex = 1.5, col = "tomato2")
text(0.5, 0.90, paste0("Treatment Surplus: ", format(sum(treatment) - sum(control), nsmall = 2, big.mark = ",")), xpd = TRUE, font = 2, cex = 1.5, col = "forestgreen")
text(0.5, 0.75, paste0("Mean Control: ", format(round(mean(control), 2), nsmall = 2, big.mark = ",")), xpd = TRUE, font = 2, cex = 1.5, col = "steelblue2")
text(0.5, 0.70, paste0("Mean Treatment: ", format(round(mean(treatment), 2), nsmall = 2, big.mark = ",")), xpd = TRUE, font = 2, cex = 1.5, col = "tomato2")
text(0.5, 0.65, paste0("Mean Treatment Surplus: ", format(round(mean(treatment) - mean(control), 2), nsmall = 2, big.mark = ",")), xpd = TRUE, font = 2, cex = 1.5, col = "forestgreen")
text(0.5, 0.55, "_______________________", xpd = TRUE, font = 2, cex = 1.5, col = "gray70")
text(0.5, 0.45, paste0("Mean Value at Stake: ", format(round(t.test(treatment, control, paired = TRUE)$estimate, 2), nsmall = 2, big.mark = ",")),
xpd = TRUE, font = 2, cex = 1.5, col = "forestgreen")
text(0.5, 0.35, paste0("Corresponding P-Value: ", format(round(t.test(treatment, control, paired = TRUE)$p.value, 2), nsmall = 2, big.mark = ",")),
xpd = TRUE, font = 2, cex = 2.0, col = "gray30")
text(0.5, 0.25, ifelse(t.test(treatment, control, paired = TRUE)$p.value < 0.05, "Mean Value at Stake is statistically significant", "Mean Value at Stake is not statistically significant"),
font = 2, cex = 1.0, col = "gray50")
text(0.5, 0.15, "**********", font = 2, cex = 1.5, col = "gray70")
----
... generating the following graphical output: