Training of the neural network model
As of right now, we are ready to train the neural network model completely within the SAP Analytics Cloud infrastructure in an R widget framework.
For this purpose the evaluation data set has been derived from the training data and used to monitor the progress of the neural network training.
You can see the semantics of this evaluation set and the training progress loop in the code snippet below:
----
require(nnet)
set.seed(42)
test_ids <- sample(1 : nrow(dta), size = 300, replace = FALSE)
test_set <- dta[test_ids, ]
train_set <- dta[-test_ids, ]
x_mean <- mean(train_set$x); x_sd <- sd(train_set$x)
y_mean <- mean(train_set$y); y_sd <- sd(train_set$y)
train_set$x <- (train_set$x - x_mean) / x_sd
train_set$y <- (train_set$y - y_mean) / y_sd
test_set$x <- (test_set$x - x_mean) / x_sd
test_set$y <- (test_set$y - y_mean) / y_sd
set.seed(42)
eval_ids <- sample(1 : nrow(train_set), size = 500, replace = FALSE)
eval_set <- train_set[eval_ids, ]
train_set <- train_set[-eval_ids, ]
metrics <- data.frame()
for (i in 1 : 100) {
set.seed(1337)
nn <- nnet(y ~ x, data = train_set, size = 40, maxit = i, linout = TRUE, rang = 0.7)
RMSE_train <- sqrt(mean((train_set$y - predict(nn))^2))
RMSE_eval <- sqrt(mean((eval_set$y - predict(nn, newdata = eval_set))^2))
metrics <- rbind(metrics, data.frame(RMSE_train, RMSE_eval))
}
plot(1 : nrow(metrics), metrics$RMSE_train, type = "l", col = "green2", lwd = 2,
main = "Training vs. Evaluation RMSE", xlab = "Iteration", ylab = "RMSE", las = 1)
lines(1 : nrow(metrics), metrics$RMSE_eval, col = "red", lwd = 2, xpd = TRUE)
legend("topright", legend = c("train", "eval"), fill = c("green2", "red"), border = NA, bty = "n")
abline(v = which.min(metrics$RMSE_eval), col = "steelblue4", lty = 2)
title(sub = which.min(metrics$RMSE_eval))
----
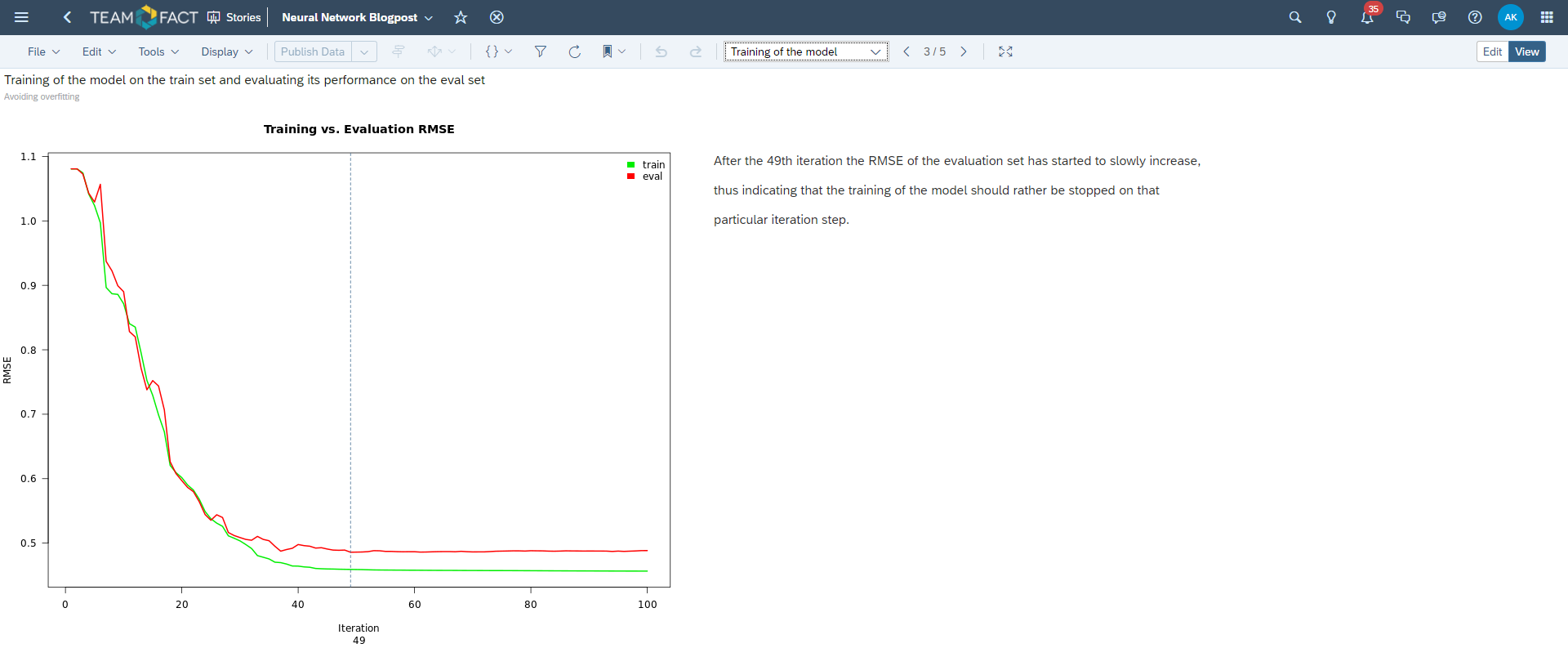
The corresponding result of this process is depicted in the plot below. Please note that the 49th iteration of this fully connected feed forward neural network presents the minimum for the loss function on the evaluation data set and, thus, should be considered as a pivotal point of the training progress.
The training should be stopped at this particular iteration.
This technique is called cross-validation and serves as a means to avoid overfitting of the underlying training data set: